La Relatividad y la Mecánica Cuántica no se pueden aplicar al mismo tiempo, al mismo problema. Al tratar de hacerlo, uno se encuentra con contradicciones. Las contradicciones surgen desde los aspectos fundamentales de cada teoría: localidad, causalidad y determinismo en la Relatividad vs. enredamiento, eventos anti-causales y resultados probabilísticos en la Mecánica Cuántica. Décadas de elaboración sobre estos aspectos encuentran su origen en un trabajo de Einstein, Podolsky y Rosen [1], que llegó a conocerse como la paradoja EPR, trabajo que busca responder la cuestión de si la Mecánica Cuántica era o no una teoría completa.
La contradicción se explica mejor en el experimento pensado de Bohm [2]. En éste, se concluye que los resultados de mediciones realizadas sobre objetos distantes se afectan entre sí instantáneamente, cuando estos objetos están enredados.
De acuerdo a la Mecánica Cuántica, el enredamiento ocurre cuando un conjunto de dos o más partículas puede describirse solamente como un todo, y no como entidades individuales. Esto parece obligar al estado de cada partícula a depender del estado de las demás, incluso cuando están ampliamente separadas.
Las consecuencias del enredamiento parecen contradecir el principio de causalidad local que impone en el espacio-tiempo la Relatividad Especial: una secuencia de causa y efecto que constituye un principio fundamental mediante el cual guiamos nuestro pensamiento y hacemos nuestro trabajo científico. Lo que exige la Relatividad Especial es una estructura causal del espacio-tiempo en forma de conos de luz (cf. Fig. 1); esta estructura impide que un evento influya sobre otro evento que ocurra fuera de su cono de luz futuro (cf. Fig. 2).
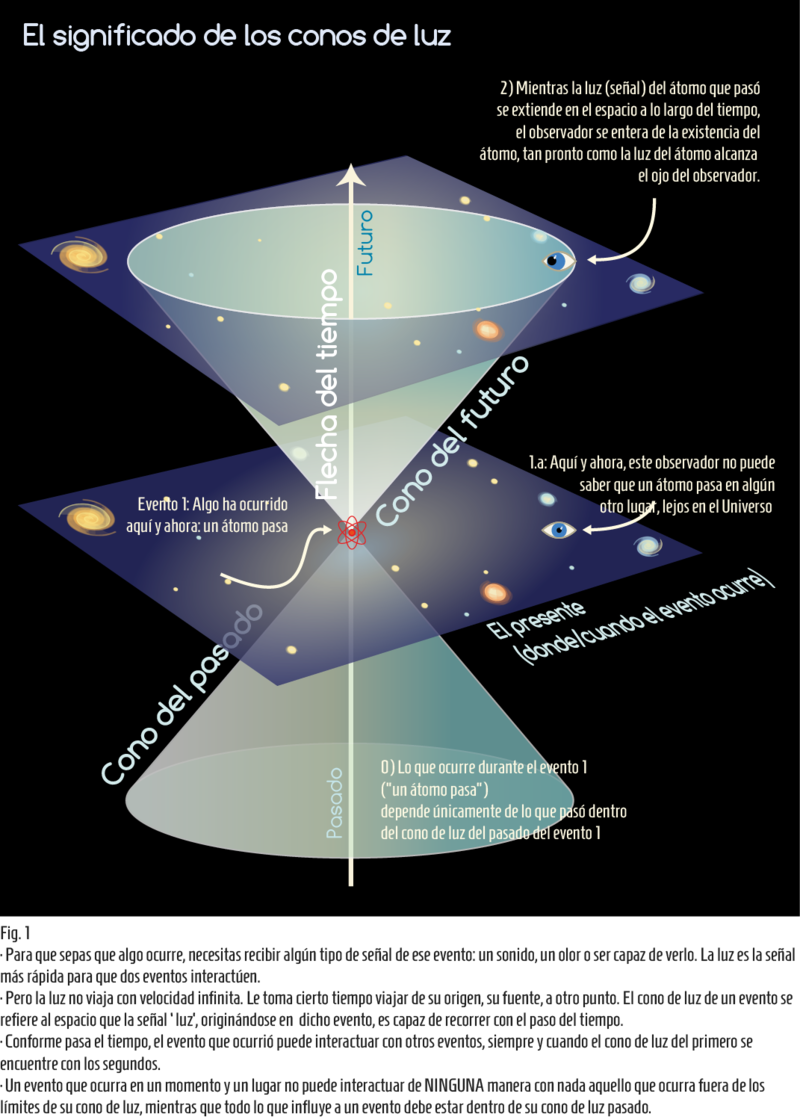
Dar click aquí para agrandar Fig. 1
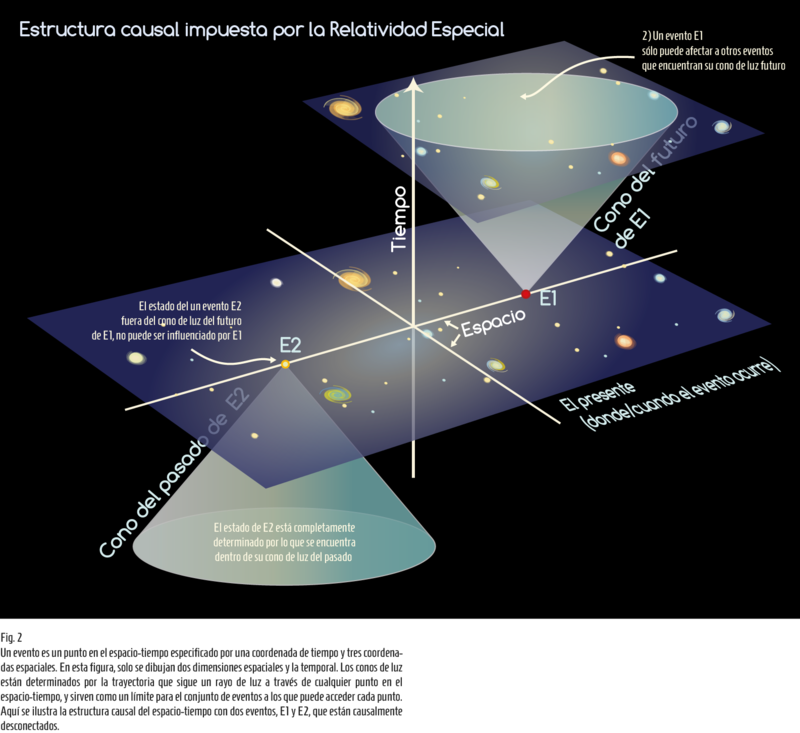
Dar click aquí para agrandar Fig. 2
Una solución propuesta para el comportamiento no-local integrado en los sistemas cuánticos es la existencia de variables ocultas. Las variables ocultas son parámetros que determinan el comportamiento de nuestro objeto de estudio, pero que no hemos tomado en cuenta; es en este sentido que están “ocultas”. Poco después de que fuera propuesto el experimento pensado de Bohm, en 1964, John Bell [3] demostró que la esperanza de completar a la Mecánica Cuántica mediante variables ocultas locales estaba perdida.
Bell construyó una desigualdad que todas las teorías de variables ocultas (locales) deben satisfacer, y demostró que la Mecánica Cuántica violaba esta desigualdad, concluyendo que es imposible explicar los fenómenos no locales de la Mecánica Cuántica echando mano de variables ocultas locales. La consecuencia de la conclusión de Bell es muy extraña: el hecho de que materia en algún planeta del universo podría saber cómo “comportarse”, a través de instrucciones dadas por materia en algúno otro planeta distante del universo; y peor aún, ¡puede saberlo de forma instantánea!
Pero desde Bell hay algo en la Mecánica Cuántica que no se ha tomado en cuenta: la factualidad, que es una consecuencia del determinismo. En un artículo recientemente publicado por Natalia Sánchez Kuntz y Eduardo Nahmad-Achar [4] esta condición fue tomada en cuenta. Hacerlo implicaría asumir que una partícula evoluciona desde el estado A, en un tiempo t0, al estado B, en el tiempo t1, de una manera determinista, es decir, que uno puede predecir el estado B dadas las suficientes condiciones iniciales; y que si el estado B tuvo lugar al tiempo t1, éste es el único estado que el sistema podría haber tomado, dadas sus condiciones iniciales al tiempo t0 (cf. Fig. 3). Pero algunas de las condiciones podrían estar todavía ocultas en forma de variables ocultas, sólo que ahora la evolución sería verdaderamente determinista.
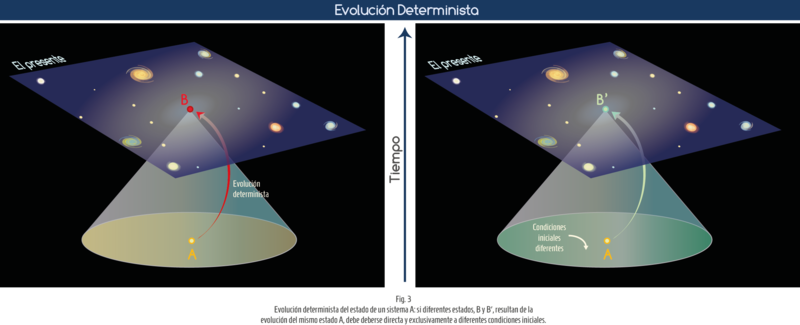
Click aquí para agrandar Fig. 3
Entonces, ¿por qué es que, al realizar repetidamente el mismo experimento, la Mecánica Cuántica no siempre da los mismos resultados? En otras palabras, por qué solo proporciona una interpretación estadística de los fenómenos naturales? Aquí debemos enfatizar una vez más el hecho de que el espacio-tiempo está dotado de una estructura causal local. Esto significa que todo lo que puede afectar un evento determinado E, debe estar dentro de su cono de luz pasado. En un momento dado t0, entonces, sólo podríamos tener acceso a las condiciones iniciales en la hipersuperficie t = t0 que están contenidas dentro del cono de luz pasado de E (ver Fig. 4). Cualquier información fuera de esta región, desconocida para nosotros, puede afectar y seguramente afectará la evolución futura del evento.
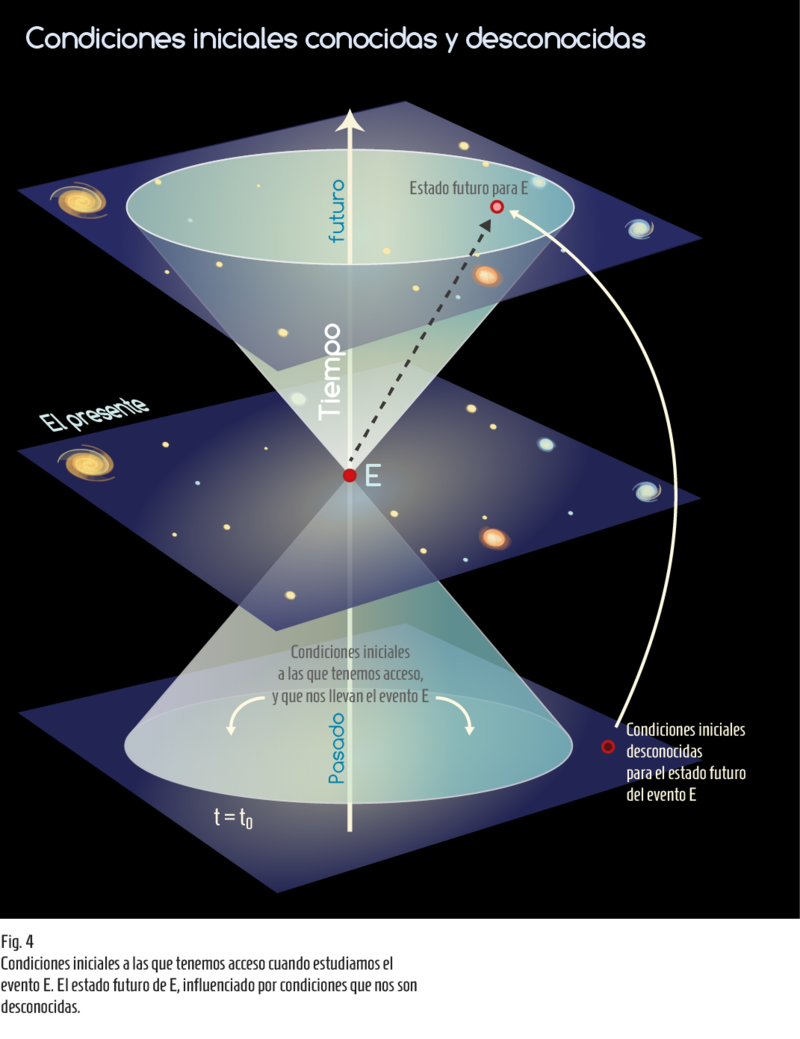
Click aquí para agrandar Fig. 4
Lo que subyace en la propuesta de los autores es que Bell hizo algunas suposiciones para construir su desigualdad que no son ciertas en un escenario determinista; cuando se agrega un verdadero determinismo a la evolución de las partículas, la desigualdad de Bell no se puede construir. Ahora, dado que la desigualdad de Bell no se puede construir, ya no existe la restricción previa que la Mecánica Cuántica debe cumplir para ser explicada localmente.
Además, uno puede construir una cierta desigualdad que todo sistema local determinista debe satisfacer. Esto se hace en el artículo citado anteriormente, y se demuestra que la Mecánica Cuántica siempre satisface esta desigualdad. De esta forma, concluyen Nahmad y Sánchez, los fenómenos que surgen del formalismo de la Mecánica Cuántica se pueden interpretar de manera local al agregar determinismo, y así adherirse a los requisitos de, al menos, la Relatividad Especial (si aún no la Relatividad General).
¿Y qué hay del enredamiento? Es importante destacar que el enredamiento, en un escenario determinista, siempre requiere de una causa común, a partir de la cual surge el comportamiento de los sistemas enredados en un momento dado, independientemente de cuán lejos estén los dos sistemas entrelazados el uno del otro. Esto siempre es posible debido al hecho de que los conos de luz de los eventos, esos puentes que conectan todo a su pasado causal, necesariamente se cruzan al retroceder en el tiempo (cf. Fig. 5).
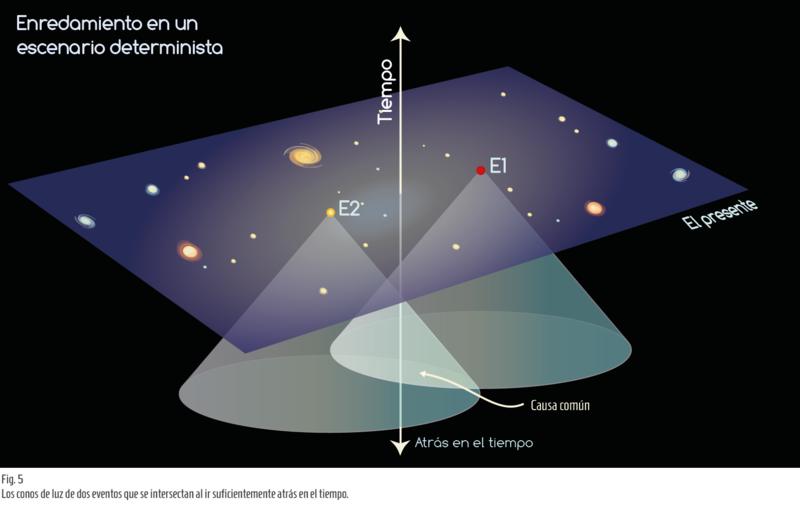
Click aquí para agrandar Fig. 5
Agradecimientos:
Los autores desean agradecer a Aline Guevara de la Unidad de Comunicación de la Ciencia del ICN, UNAM, por las imágenes en este trabajo.
Referencias
[1] A. Einstein, B. Podolsky and N. Rosen: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935).
[2] D. Bohm and Y. Aharonov: Discussion of experimental proof for the paradox of Einstein, Rosen, and Podolsky, Phys. Rev. 108, 1070 (1957).
[3] J.S. Bell: On the Einstein Podolsky Rosen paradox, Physics 1, 195 (1964).
[4] N. Sánchez-Kuntz and E. Nahmad-Achar: Quantum Locality, Ring’s a Bell?: Bell’s inequality meets local reality and true determinism, Found. Phys. 48, 27 (2018). doi: 10.1007/s10701-017-0126-z





