Marcus du Satoy, un profesor de matemáticas de la Universidad de Oxford famoso por conducir la serie documental “The Code” de la BBC, alguna vez dijo: “El poder de las matemáticas con frecuencia radica en su capacidad de cambiar una cosa en otra, cambiar la geometría en lenguaje”. Ese parece ser justo el trabajo del físico Hernando Quevedo Cubillos, investigador del Departamento del Instituto de Ciencias Nucleares, UNAM: él transmuta el lenguaje matemático en teorías de la física contemporánea, y viceversa.
En diciembre del año pasado, la revista Journal of Mathematical Physics incluyó un artículo de Hernando Quevedo, titulado “Geometrotermodynamics”, entre los diez más citados en el período de 2006 a 2018. El texto apareció en 2007, pero al principio no todo fue viento en popa: como en el artículo Quevedo planteaba una idea nueva, una transmutación físico-matemática con aplicaciones a la química, se recibió con reserva. Después, en 2008, Hernando Quevedo publicó un segundo artículo titulado “La geometrotermodinámica de los agujeros negros”. Este segundo texto recibió una atención importante por parte de los investigadores de las áreas de teoría de campos y relatividad.
El área de la física teórica que él mismo denominó se conoce como geometrotermodinámica o GTD.
Sistemas termodinámicos
Para poder abordar esta área, es importante introducir los sistemas termodinámicos, que consisten en “una parte del Universo que se aísla para su estudio”, en este caso, para su modelado matemático. En física un sistema termodinámico es un conjunto, de identidad fija, alrededor del cual se puede establecer un límite. Los límites pueden ser fijos o cambiar. Todo fuera del límite, es el entorno o los alrededores.
Las variables termodinámicas o variables de estado son las magnitudes que describen el estado de un sistema termodinámico. En el caso de un gas, por ejemplo, las variables pertinentes para caracterizarlo termodinámicamente son la masa, el volumen, la presión y la temperatura. Un sistema se encuentra en equilibrio termodinámico cuando sus variables se mantienen constantes con el tiempo.
Un ejemplo de un sistema termodinámico es el gas ideal, representado por las ecuaciones de estado:
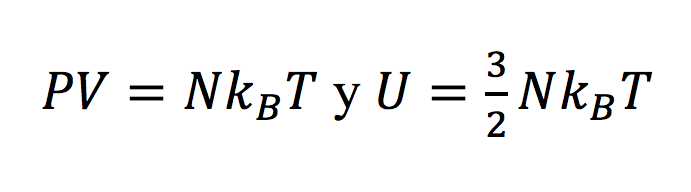
Donde las variables consideradas son P, la presión; V, el volumen; N, el número de partículas; T, la temperatura absoluta, y U, la energía interna. kB es la constante de Boltzmann.
El gas ideal es un gas teórico en el que la interacción entre sí de sus partículas puntuales, mientras éstas se mueven aleatoriamente, se traduce únicamente en energía cinética (sin convertirse en otra forma de energía como el calor o la energía potencial).
Lo que pocos saben es que las ecuaciones de estado son equivalentes a la ecuación fundamental del gas ideal siguiente (en la que S es la entropía), donde N es constante:
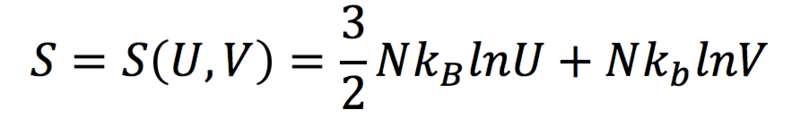
La importancia de esta ecuación fundamental reside en que a partir de ella uno puede obtener toda la información del sistema termodinámico. Esto que se hizo para el gas ideal se puede generalizar a cualquier sistema termodinámico, que tendrá su ecuación fundamental asociada.
De la termodinámica a la geometría, y de vuelta
Ahora cabe hacernos las siguientes preguntas: ¿es posible describir las propiedades del gas ideal, o de cualquier sistema termodinámico, mediante el estudio de las propiedades geométricas de algún espacio u objeto geométrico? ¿Es posible, teniendo en cuenta las propiedades geométricas de tal espacio, llamémosle espacio de equilibrio, hablar de termodinámica? Si respondemos que sí, obtenemos una especie de diccionario GTD en el que tenemos equivalencias entre la geometría (en particular, la diferencial, que aborda las formas geométricas -especialmente las curvas y las superficies- mediante el análisis matemático) y la termodinámica:
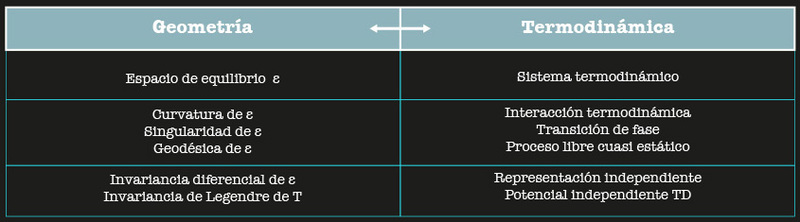
Lo que aporta la GTD al estudio de los sistemas termodinámicos es que se puede dar una representación geométrica de éstos, aplicar todas las nociones del formalismo geométrico, para después regresar a la termodinámica.
Para ilustrar lo anterior regresemos al ejemplo del gas ideal. En este caso podemos obtener una distancia, una métrica, a partir de su ecuación fundamental y sus derivadas:
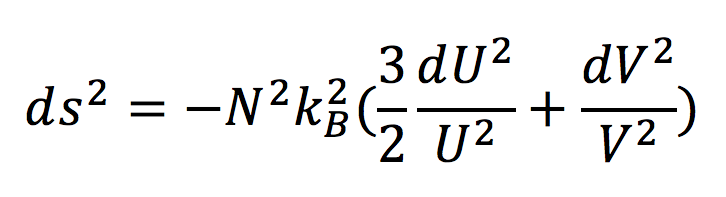
donde las coordenadas son U, la energía interna, y V, el volumen del gas ideal. Al calcular la curvatura correspondiente a este espacio de equilibrio, obtenemos cero. Este espacio es plano, lo cual indica que no hay interacción termodinámica.
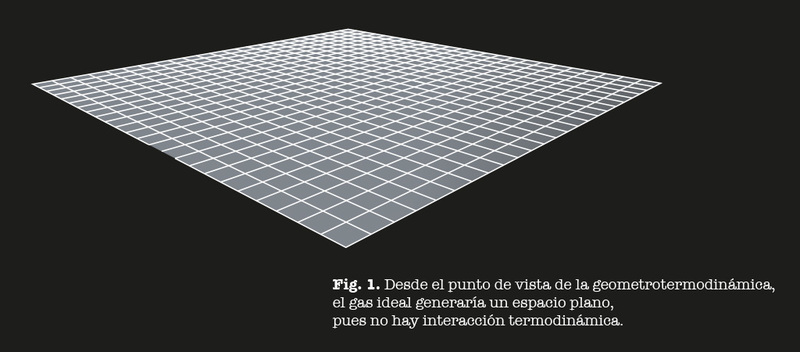
Fig. 1 Desde el punto de vista de la geometrotermodinámica, el gas ideal generaría un espacio plano, pues no hay interacción termodinámica
Desde este punto de vista, el gas ideal es muy parecido a la métrica de Minkowski en relatividad. Este es el sistema más simple que podemos estudiar desde el punto de vista de la GTD.
Geometrotermodinámica del agua
Hay sin duda casos más interesantes que el gas ideal por estudiar. El agua se puede considerar, bajo ciertas condiciones, como un fluido de Van der Waals. Es interesante porque tiene transiciones de fase (puede pasar a sólido, líquido o gaseoso). Tomamos la ecuación fundamental:
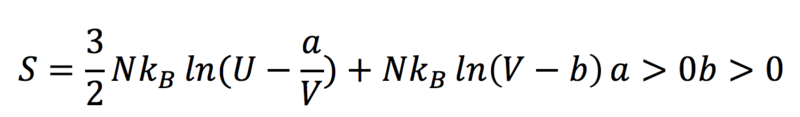
A partir de esta ecuación, se obtiene la métrica del agua:
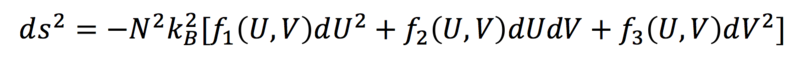
A partir de esta métrica podemos obtener la geometría del agua, sin duda mucho más complicada que la del gas ideal, pues como se mencionó antes, sí tiene transiciones de fase, es decir, tiene interacción termodinámica.
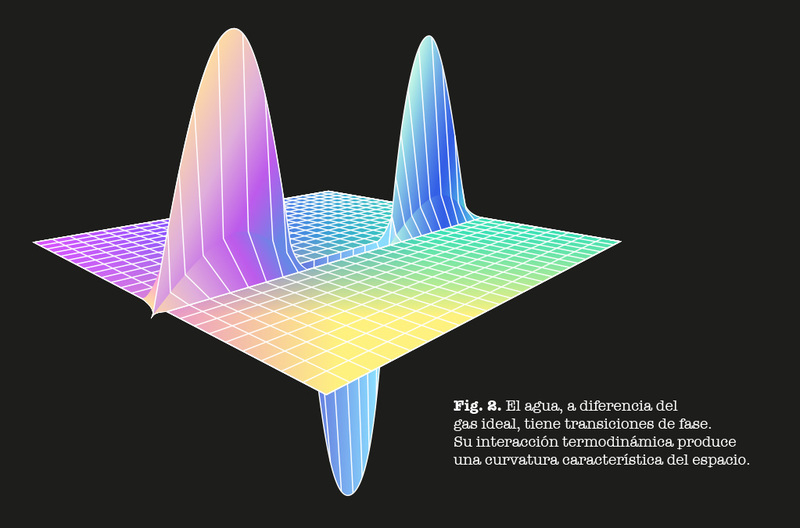
Fig. 2 El agua, a diferencia del gas ideal, tiene transiciones de fase. Su interacción termodinámica produce una curvatura característica del espacio
Otros sistemas termodinámicos
Otros sistemas que se pueden estudiar desde el punto de vista de la GTD, que Hernando Quevedo y sus colaboradores han investigado durante los últimos diez años, son los siguientes:
- Microsistemas: sistemas con spin, gases cuánticos, condensados de Bose-Einstein.
- Sistemas ordinarios: gas ideal, gases reales, líquidos, reacciones químicas.
- Sistemas exóticos: sistemas económicos, sistemas sociales, objetos relativistas compactos como agujeros negros, estrellas de neutrones y enanas blancas, objetos relativistas.
- El Universo.
En todos estos sistemas, hacer geometría es equivalente a hacer termodinámica, es decir, se ha demostrado en todos estos ejemplos que el formalismo de la GTD funciona.
Algunos ejemplos interesantes
- Geometrotermodinámica de hoyos negros: de acuerdo con Stephen Hawking, si se conoce el área del horizonte de eventos de un agujero negro, se puede postular que dicha área es proporcional a la entropía. Y si se tiene la entropía, es posible conocer la termodinámica. En el caso del agujero negro más general que existe en la teoría de Einstein, al igual que en otras teorías generalizadas, se demostró que la GTD se puede utilizar como método alternativo para explorar las propiedades termodinámicas de los hoyos negros.
- Geometrotermodinámica aplicada al Universo: se demostró que a partir de la GTD se obtiene una ecuación fundamental que, junto con la teoría de la relatividad de Einstein, describe la evolución del Universo desde la época de la inflación (10^{-36} segundos) hasta nuestros días (13.8 mil millones de años). Además, predice la existencia de transiciones de fase para las épocas anteriores a la inflación.
Dra. Gabriela Frías Villegas/Unidad de Comunicación de la Ciencia
Edición, web e ilustración: Mtra. Aline Guevara Villegas/Unidad de Comunicación de la Ciencia
Asesoría científica: Dr. Hernando Quevedo Cubillos y Dr. César López Monsalvo




