El Dr. López Vieyra inició el coloquio de divulgación del ICN del mes de enero, con una descripción general del problema de los tres cuerpos, que es un problema clásico que surgió desde el inicio de la mecánica newtoniana. Dicho problema tiene que ver con la antigua pregunta de cómo se mueve el sistema compuesto por el Sol, la Tierra y la Luna.
En la física y en las matemáticas siempre se trata de reducir este tipo de problemas a situaciones idealizadas. Entonces, se considera, en primera aproximación, que los cuerpos son partículas puntuales, con una cierta masa, y se trata de dar una descripción simple del problema. Al tener un modelo simplificado, surge la pregunta de si es posible resolver las ecuaciones de Newton para describir el movimiento de tal sistema en primera instancia.
Recuento histórico
En el recuento histórico que hizo el Dr. López Vieyra, recordó que, en la mecánica newtoniana, el problema de los tres cuerpos consiste en tomar las posiciones y velocidades iniciales de tres masas puntuales y resolver las ecuaciones para sus movimientos subsecuentes de acuerdo a las leyes del movimiento de Newton. En particular, se trata del problema de resolver el movimiento de tres partículas bajo su atracción gravitacional mutua.
El Dr. López Vieyra planteó la siguiente pregunta: ¿es posible resolver el problema newtoniano de los tres cuerpos? Generalmente se piensa que no es posible. Sin embargo, el Dr. López Vieyra mencionó que esta es una visión errónea y que es parte del folklore científico de nociones imprecisas.
El problema de los tres cuerpos es un caso particular del problema de los n cuerpos en interacción gravitacional. Este problema surgió cuando Newton publicó en 1687 su obra maestra Principia Matemática, donde publicó la ley de gravitación universal, dada por la ecuación
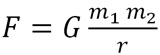
Es importante mencionar que la teoría de Newton predice correctamente las leyes de Kepler para el movimiento planetario en el caso de dos cuerpos. Entonces, cabe hacernos la siguiente pregunta: ¿son suficientes las leyes de Newton para entender el movimiento de los cuerpos celestes en el espacio? En un principio pareciera que sí. Pero, al preguntarse sobre esto, Newton se dio cuenta de que el problema era muy difícil y que de hecho pareciera que el mismo Sistema Solar fuera inestable.
De acuerdo con el Dr. López Vieyra, para entender el problema de los tres cuerpos, es importante recordar un caso más simple, es decir, el problema de los dos cuerpos. Éste consiste en tratar de predecir el movimiento de dos partículas con masas m1 y m2 que se mueven en un espacio euclidiano tridimensional interactuando a través de sus leyes newtonianas de atracción mutua. El problema de los dos cuerpos puede describirse por un sistema de ecuaciones diferenciales ordinarias acopladas.
Un método usual para resolver este tipo de sistemas es encontrar primeras integrales que reducen la dimensionalidad del espacio fase. El problema de dos cuerpos es un sistema que es maximalmente superintegrable, lo que explica que todas las trayectorias acotadas sean periódicas. Para entender la noción de superintegrabilidad, es importante recordar la noción de integrabilidad de Liouville.
Para un sistema Hamiltoniano con n grados de libertad y dimensión en el espacio de fase igual a 2n, si existen n integrales de movimiento l(p,q) en involución tal que

se dice que el sistema es integrable. Si existen más de n integrales de movimiento de modo que
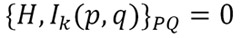
se dice que el sistema es superintegrable. Si existen 2n-1 integrales, se dice que el sistema es maximalmente superintegrable. Este último es el caso de dos cuerpos en interacción gravitacional.
De acuerdo con el Dr. López Vieyra, si un sistema de dos cuerpos en interacción gravitacional tiene trayectorias elípticas, hiperbólicas y parabólicas, se le puede dar una solución exacta. No obstante, si se agrega la influencia de un cuerpo más, parecería que, encontrar una solución exacta es imposible. Por ello, el problema de los tres cuerpos se volvió una obsesión para muchos de los grandes matemáticos, como Leonhard Euler, Joseph Louis Lagrange, Jean Baptiste d’Alambert, Henri Poincaré, Sofía Kowaleskaya y Karl Weierstrass, entre otros.
Algunos de ellos encontraron soluciones para casos particulares. La primera de ellas se la debemos a Leonard Euler, quien resolvió el problema de los dos cuerpos con gran detalle. Después de resolverlo, se enfocó en el problema general de los tres cuerpos y encontró una solución analítica y periódica. En esta solución, tres masas se mueven de modo que siempre son colineales y que sus movimientos ocurren en tres órbitas elípticas diferentes.
Como comentó el Dr. Vieyra, tres años después Lagrange encontró otra solución periódica al problema general de los tres cuerpos, en la que la configuración es un triángulo equilátero donde los cuerpos están colocados en sus vértices. De nuevo, a pesar de que cada cuerpo se mueve en su propia órbita elíptica, la forma de la configuración central se preserva, a pesar de que el tamaño del triángulo cambia en el tiempo.
Como el problema es tan complicado, se trataba de hacer alguna aproximación para resolverlo, y la más natural es suponer que hay dos cuerpos muy pesados con masas m1 y m2 y un tercer cuerpo con una masa m3 más pequeña. A esta aproximación se le llama el “Problema de los tres cuerpos restringido”. Aunque este problema no se puede resolver analíticamente, hay soluciones numéricas a dicho problema que son muy útiles, pues se pueden usar para poner en órbita a satélites, en trayectorias que sean más o menos estables.
De acuerdo con el Dr. Vieyra, para finales del siglo XIX, se consideraba que la solución al problema de n cuerpos era muy importante, por ello, en el Acta Mathematica de 1885 se anunció un premio para celebrar el cumpleaños 60 del rey Oscar II de Suecia, para aquel que pudiera resolverlo. Finalmente, el matemático francés Henri Poncaré ganó la competencia al demostrar que no existe una solución analítica general para el problema, dada por expresiones algebraicas e integrales. Lo que en realidad encontró Poincaré es que se trata de un sistema caótico.
Sin embargo, algunos años después, el físico Finlandés Karl Sundman encontró soluciones para el problema de los tres cuerpos, que se expresaban como series convergentes de potencias de
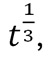
para casi todas las condiciones iniciales, excepto para aquellas en las que el momento angular es cero. Con este descubrimiento, Sundman había resuelto el problema planteado originalmente por el matemático alemán Karl Weierstrass para la competencia por el premio anunciado en Acta Mathematica. Desafortunadamente, la convergencia de las soluciones es muy lenta, lo que hace que éstas sean inútiles para aplicaciones prácticas. Se necesitan millones de términos para poder describir la evolución del sistema aun para intervalos de tiempo muy cortos.
A partir de esta discusión podemos concluir que el problema de los tres cuerpos no es insoluble, pero que no se puede resolver por el método usual de encontrar primeras integrales. Entonces, la pregunta es la siguiente: ¿habrá una contradicción con la noción del caos? La respuesta es que no, pues cuando tomamos en cuenta los errores de redondeo, éstos hacen que la serie sea irresoluble, es decir, su evolución en el tiempo es impredecible.
Trayectorias en forma de ocho
En 1993 ocurrió un descubrimiento inesperado: Christopher Moore del Instituto de Santa Fe encontró mediante experimentos numéricos que en el caso gravitacional existe una solución en la que tres cuerpos de la misma masa se mueven en una misma trayectoria en forma de ocho. Posteriormente, en el año 2000, los matemáticos Alain Chenciner (Universidad de Paris) y Richard Mongomery (Universidad de California) redescubrieron esta solución y probaron rigurosamente su existencia. En particular, encontraron que la trayectoria es una curva transcendental. C. Simó (Universidad de Barcelona) llamó a esta solución “coreografía”. Además de las coreografías de tres cuerpos, y con técnicas numéricas más elaboradas, Simó encontró coreografías de cuatro cuerpos, por ejemplo, en la trayectoria llamada “súper ocho”, y cientos de coreografías de formas muy caprichosas con más cuerpos. Es interesante mencionar que en 2017 Shijun Liao y Xiaoming Li (Universidad de Shangai) encontraron más de mil soluciones periódicas al problema de los tres cuerpos, usando un código computacional numérico muy avanzado.
El problema inverso: coreografía 3B en la lemniscata
¿Existirán algunas curvas que conozcamos de manera exacta en las que podamos encontrar movimientos como aquellos descritos anteriormente? En 2003 T. Fujiwara, H. Fukuda y H. Ozaki (Japón) descubrieron una coreografía de tres cuerpos en una curva algebraica que se llama lemniscata de Bernoulli descrita por la ecuación siguiente:
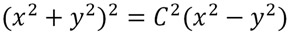
y encontraron el potencial para el cual ese movimiento de tres partículas es una solución de las ecuaciones de Newton. Entonces, con esto se resolvió el problema inverso en mecánica clásica: supusieron cuál era el movimiento y encontraron el potencial.
La conjetura de Alexander Turbiner
Entre otras cosas, el Dr. Vieyra también comentó en su plática que el doctor Alexander Turbiner (ICN-UNAM) propuso en 2013 la conjetura de que, en la Mecánica clásica, cualquier trayectoria periódica cerrada debe ser particularmente superintegrable. Es decir, que si existen suficientes integrales, pero únicamente a lo largo de la trayectoria.
Conclusiones
El Dr. López Vieyra finalizó el coloquio con las conclusiones siguientes:
Una coreografía de tres cuerpos en una curva en forma de ocho, con momento angular cero, existe para un conjunto de potenciales de pares de partículas que son al mismo tiempo repulsivos y atractivos en pequeñas distancias, y atractivos solamente para el caso de distancias grandes.
Se ha conjeturado que todas estas trayectorias en forma de ocho son maximalmente superintegrables.
Ya se sabe que una coreografía de cinco cuerpos existe y es una solución de las ecuaciones de Newton para el caso gravitacional. ¿Será válida la conjetura de Turbiner en este caso?
El coloquio del Dr. Juan Carlos López Vieyra se puede ver en la liga siguiente: https://youtu.be/TopUK5MNzPk





